Part 6. Are M&S outputs real?

TL; DR

1. Once the model is suitably validated, it will predict the therapy’s efficacy. This prediction is based on knowledge that science assumes real, and applied to virtual data, that profiles the virtual patients. As a matter of fact, the way virtual patients are designed and validated, make them represent real patients who may benefit from the therapy if proven effective.

2. Efficacy prediction with M&S is not less “real” than efficacy estimation with a RCT. Main differences between in silico and RCT are:

• unlimited sample size in in silico approach

• Conducting RCT is a very complicated process with many challenges
• The main limitations of an RCT are the external generalizability and the weakness to detect adverse events that are then later detected during phase IV, which increasingly leads to market withdrawal.

Often the first thing a person questions who is presented with the M&S approach is the reality of the simulation results.

The notions of reality and real things are the subject of a debate as old as humanity and philosophy. A debate which tries to reconcile the perception that ordinary peoples have and the thinkings of philosophers and scientists.

So as not to enter into this debate, we will compare two means of approaching the same reality in our sphere of interest, the efficacy of a new therapy.

Before getting to the core of this comparison, an example from history will be employed to introduce this topic: Eratosthenes, due to an indisputable sense of observation and a model of reality built from knowledge in astronomy and geometry of the moment, obtained by calculation almost 23 centuries ago a value of the Earth's circumference that we can consider to be (roughly) real (see Box 9).

Box 9: an old demarch: reasoning, use of knowledge, mathematical modeling and observation to approach reality

Eratosthenes deduced the circumference of the Earth in a purely geometric way around 230 BC. He considered the sun's light rays to be parallel at any point on the earth, because the sun was very large compared to the earth and very far away. He compared the observation he made on the shadow of two objects located in two places, Syene and Alexandria, considered to be on the same meridian, which was approximately correct, on June 21 (summer solstice) at noon. It is at this precise time of the year that in the northern hemisphere the sun occupies the highest position above the horizon. Now, in a previous observation, Eratosthenes had noticed that there was no shadow, at that time, in a well in Syene (a town located roughly on the Tropic of Cancer). So at this time and at this precise place, the sun was vertical and its light directly illuminated the bottom of the well. Eratosthenes noticed, however, that on the same day at the same time a year later, a gnomon located in Alexandria had a shadow. The sun was therefore not there vertically. The shadow and the gnomon formed the sides of a right triangle whose solar radius was the hypotenuse. Eratosthenes therefore deduced by geometry that the angle between the solar ray and the vertical there was 7.2 degrees (our degrees). He estimated then the distance between Syene and Alexandria to be about 5,000 stadia. It is said that he used for this evaluation the average duration of the journey by the caravans of camels between the two towns and the observation that the speed of a camel is constant. Eratosthenes proposed a simple model of what he had observed: a circle (section of the earth along the meridian joining Alexandria to Syene, the earth was said to be spherical since at least Aristotle's observations on eclipses and Strabon’s one on the horizon which prevents navigators from seeing the distant lights), the angle of the two rays joining the center of the circle to, on the one hand, the well of Syene and on the other hand the gnomon of Alexandria was the same 7.2 degrees because of the geometric theory of congruent alternate-interior angles. To this angle therefore corresponded 1/50 of the circumference of the earth, the arc connecting Syene in Alexandria, an arc measuring 5,000 stadia. The circumference of the Earth was estimated at 250,000 stadia, or about 39,600 km, very close to the value accepted today.

This story illustrates that a reality can be the result of a calculation and that by calculation man builds a new layer of reality.

A model of disease and therapy will be more complicated than the model of Eratosthenes, but in essence it is the application of the same reasoning. Once the model is suitably validated, it will predict the therapy’s efficacy. This prediction is based on knowledge that science assumes real, and applied to virtual data, that profiles the virtual patients. As a matter of fact, the way virtual patients are designed and validated, make them represent real patients who may benefit from the therapy if proven effective.

Measures of the effectiveness of this therapy obtained through the application of the model on the virtual population may differ from those obtained through the use of the gold standard, the randomized controlled clinical trial (RCT), applied to a real population.

The RCT methodology is rigorous in that it is designed to avoid bias. But even when strictly applied, results retain some uncertainty, due to the rate of false positives (a rather rare case if the statistical analysis is applied correctly) and false negatives (if the magnitude of the efficacy was overestimated at the start). Other factors contributing to uncertainty that are more or less well controlled, are sample size and the imbalance between arms (thanks to the randomization, they are comparable, but only on average, never identical). Added to the questionable representativity of the trial participants, this uncertainty becomes especially important with respect to external generalizability of the efficacy measured in the trial to patients who were not included in the trial. This includes prospective patients, patients from another race or cultural environment. Let us remember Heraclitus’s quote which captures the essence of this aspect: “You could not step twice into the same river.”

The measures of efficiency for a RCT are calculations on data usually electronically collected in a database after having been recorded by a human investigator. The information carried by these data has therefore been processed through several steps from what it is supposed to represent. How do they differ in terms of both uncertainty and departure from reality from the data describing the virtual population to which the model is applied?

Compared to the RCT, the efficiency measures obtained through the model are not affected by the same sources of uncertainty. Since the model and the virtual population are validated, the uncertainty of efficacy measures primarily stems from the validation data and the accepted deviation. Factors of measurement uncertainty provided by the clinical trial on real patients, such as the sample size or the imbalance between arms, do not apply to the in silico approach. In addition, adapting the measurement to other situations will follow the same process, model and virtual population and thus uncertainty remains stable.

After this excursion to what is real and the comparison between both measures, the conclusion may be that one is probably not extremely more real than the other. And in the end, why shouldn't they both be equally real? A quote from Joseph Fourier (French mathematician, 1768 - 1830) may consolidate both approaches, the randomized clinical trial and the M&S : "... mathematical analysis can still grasp the laws of these phenomena / It makes them present and measurable to us and seems to be a faculty of human reason intended to make up for the brevity of life and the imperfection of the senses" [1].

The comparison between RCT and M&S as a tool to measure and predict clinical efficacy of a new therapy is summarized in Table 5.

Table 5: Efficacy prediction with M&S is not less “real” than efficacy estimation with a RCT.

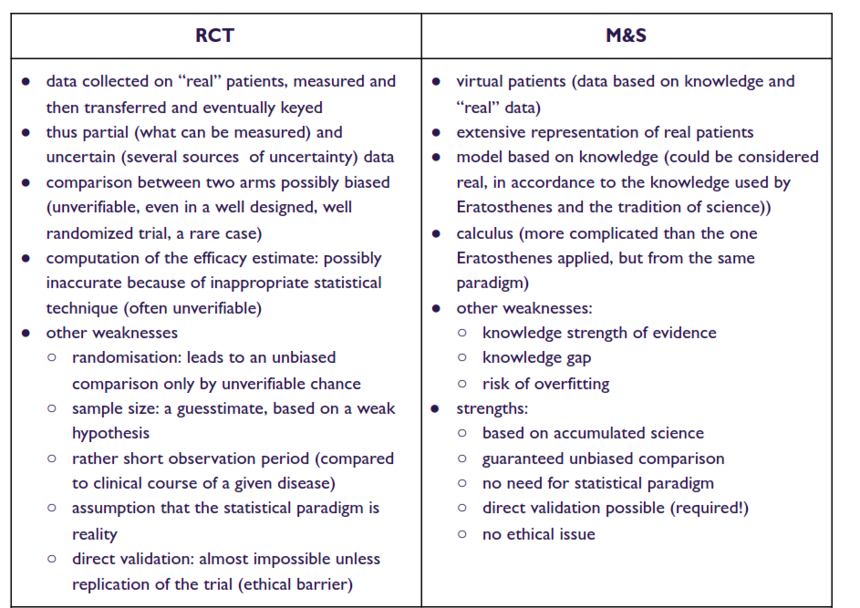
Beside the issue of uncertainty, there are other differences in the real RCT and in silico CT outputs. To quote a few:

• One of the strengths of the in silico CT is also one of its weaknesses: unlimited sample size. This allows for detection of significant differences that may not be clinically meaningful.
• Conducting a real RCT comes with several challenges. E.g. unblinding, cross-over, lack of compliance, drop-outs, missing data may result in over- or underestimation of the efficacy. Not to mention intentional circumvention of the rigors of a RCT.
• The main limitations of an RCT are the external generalizability or lack thereof and the weakness to detect adverse events that are then later detected during phase IV, which increasingly leads to market withdrawal. In silico CT manages the generalizability issue. In theory at least, it could also manage the toxicity issue. However, there is a lack of experience in this domain.